1947. Condensation
of the graph
Find the number of edges
in the condensation of a given directed graph.
The condensation of a
directed graph G is a directed graph G*, whose vertices are strongly connected
components of G, and the edge in G* is present only if there exists at least
one edge between the vertices of corresponding connected components.
The graph condensation
does not contain multiple edges.
Input. The
first line contains number of vertices n and number of edges m (n ≤ 104, m ≤ 105) in the graph. Each of the next m lines describe the edge of the graph. The i-th edge is
given with the starting bi and the ending ei (1 ≤ bi, ei ≤ n) vertex of the graph. The input graph can
contain the multiple edges and loops.
Output. Print the number of edges
in graph condensation.
|
Sample
input |
Sample
output |
4 42 13 22 3
4 3 |
2 |
SOLUTION
graphs – strongly connected
components
Algorithm analysis
Find
the strongly connected components in the graph. Color all vertices of each
strong connected component with one unique color. Let color[i] be the color of the i-th vertex. The number of used colors
equals to the number of strong connected components.
Iterate
over all the edges of the original graph. If the edge connects vertices of different
colors, then it belongs to the graph condensation. Put all the edges (a, b)
for which color[a] ≠ color[b] into the set s. Since we are using a set, not a multiset, multiple edges will
not be taken into account. The number of elements in the set s will be equal to the number of edges
in the graph condensation.
Example
The
graph shown in the example has the form:
Graph
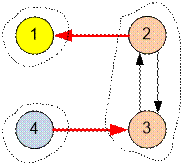
condensation contains three vertices and two edges.
Algorithm realization
Store the input graph in the adjacency list g. Store the inverse graph (the graph with
reversed edges) in the adjacency list gr.
The edges of the condensed graph will be stored in the set of pairs s.
vector<vector<int> > g, gr;
vector<int> used, top, color;
set<pair<int,int> > s;
Function dfs1 implements the depth
first search on the input graph. Put into the array top the sequence of vertices in the order in which the depth first
search finishes their processing.
void
dfs1(int v)
{
used[v] = 1;
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(!used[to]) dfs1(to);
}
top.push_back(v);
}
Function dfs2 implements the depth
first search on the reversed graph. All the vertices that will be traversed as
a result of a recursive call of the dfs2 function, belong to one strong
connected component. Color all visited vertices with color c.
void
dfs2(int v, int
c)
{
color[v] = c;
for(int i = 0; i < gr[v].size(); i++)
{
int to =
gr[v][i];
if
(color[to] == -1) dfs2(to,c);
}
}
The
main part of the program. Read the input data. Construct the reversed graph.
scanf("%d %d",&n,&m);
g.resize(n+1);
gr.resize(n+1);
for(i =
0; i < m; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
gr[b].push_back(a);
}
Run the depth first search on
the input graph. The sequence in which the processing of graph vertices is
completed is stored in the top array.
used.resize(n+1);
for(i =
1; i <= n; i++)
if (!used[i])
dfs1(i);
Run the depth first search on
the reversed graph. Iterate the vertices of the reversed graph in the order of
traversing the array top from right
to left (from the end to the beginning). The vertices included in the same
strong connected component are colored with the same color. The current paint
color is in the variable c.
color.assign(n+1,-1);
c = 0;
for(i = 1; i <= n; i++)
{
v = top[n-i];
if (color[v]
== -1) dfs2(v,c++);
}
Variable c contains the number of connected components.
for(i = 1; i < g.size(); i++)
for(j = 0; j < g[i].size(); j++)
{
to = g[i][j];
Iterate over all the edges of
the graph (i, to). Check if the vertices i
and to lie in different strongly
connected components. If
this is true, they are
painted with different colors. Then the edge (i, to)
belongs to the condensation of the graph, so insert into set s the pair (color[i], color[to]). Due to
the fact that we use a set, not a multiset, multiple pairs will not be taken
into account.
if (color[i]
!= color[to])
s.insert(make_pair(color[i],color[to]));
}
Print the number of edges in
the graph condensation.
printf("%d\n",s.size());
Java realization
import java.util.*;
class Pair implements Comparable<Pair>
{
int x, y;
Pair(int x, int y)
{
this.x = x;
this.y = y;
}
@Override
public int compareTo(Pair a)
{
if (x == a.x) return y - a.y;
return x - a.x;
}
}
public class Main
{
static
ArrayList<Integer>[] g, gr;
static int used[], color[];
static Vector<Integer> top = new
Vector<Integer>();
static TreeSet<Pair> s = new TreeSet<Pair>();
static void dfs1(int v)
{
used[v] = 1;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 0) dfs1(to);
}
top.add(v);
}
static void dfs2(int v, int c)
{
color[v] = c;
for(int i = 0; i < gr[v].size(); i++)
{
int to = gr[v].get(i);
if (color[to] == -1) dfs2(to,c);
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
gr = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
gr[i] = new ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new int[n+1];
for(int i = 1; i <= n; i++)
if (used[i] == 0) dfs1(i);
color = new int[n+1];
Arrays.fill(color, -1);
int c = 0;
for(int i = 1; i <= n; i++)
{
int v = top.get(n-i);
if (color[v] == -1) dfs2(v,c++);
}
for(int i = 1; i < g.length; i++)
for(int j = 0; j < g[i].size(); j++)
{
int to = g[i].get(j);
if (color[i] != color[to])
s.add(new Pair(color[i],color[to]));
}
System.out.println(s.size());
con.close();
}
}